Восстанавливаю старую статью.

Дали мы объявление в университете что ищем человека которому интересны свободные CAE и он готов их изучать и писать интересные статьи(естественно открытые для чтения), но видимо не судьба….
Поэтому мы начинаем перевод руководства к CAE Elmer (Elmer Tutorials), т.к. оно по виду проще.
Это собственно перевод, ниже все несколько разбавлено размышлениями и скриншотами.
Допустим вы поставили Elmer(о сборке из исходников позже), скажу лишь что в некоторых дистрибутивах он есть, так как обладает лицензией GPL.
Table of Contents
- Каталог: TemperatureGenericGUI
- Решатели: HeatSolve
- Инструменты: ElmerGUI,netgen,OpenCascade
- Размерность задачи: 3D, стационарный(установившийся) случай
Описание задачи
Этот урок пытается показать как решаются уравнения теплопереноса для некоторого 3D объекта. Твердое тело (смотри рисунок 1) нагревается внутренним источником тепла. В какой-то части температурная граница фиксируется (задана). Математически, проблема описывается уравнением Пуассона
\begin{cases} -k\Delta T = \rho f \text{ в } \Omega \\ T = 0 \text{ на } \Gamma \end{cases}
где k это коэффициент теплопроводности, T — температура, а f является источником тепла. Предполагается что плотность и теплопроводность являются константами. Чтобы решить задачу мы предполагаем, что на части границы фиксированная температура T0 = 293K , внутреннее тепло генерирует , h = 0.01 Вт/кг, и используем свойства материала алюминий.
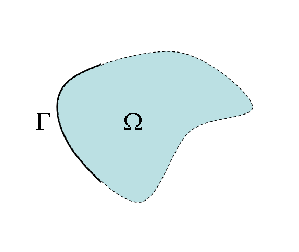
Figure 2: Рис 1:Произвольный объект нагревается
Порядок решения
Запустите ElmerGUI из командной строки или щелкнув по иконке на вашем рабочем столе. Здесь мы опишем основные шаги в ElmerGUI выписав все нажатия на пункты меню. Табуляция обычно означает что выбор делается в окне выбранном на более высоком уровне.
Заданная геометрия pump\_carter\_sup.stp в файле step формата, находиться в папке samples/step в каталоге ElmerGUI, этот файл любезно предоставлен AIM@SHAPE Репозиторий Форм INRIA. Уравнения теплопроводности идеально подходят для метода конечных элементов и решение может быть найдено даже на сетках, что для некоторых других проблем было бы невозможно. Поэтому вы можете легко экспериментировать решая эту задачу на различных сетках. Если у вас нет OpenCascade вы можете попытаться решить эту задачу с помощью grd файлов angle3d.grd, angles3d.grd, bench.grd или cooler.grd.
CAD геометрия заданная в step файлик на лету трансформировалась с помощью OpenCascade библиотеки в stl файл, для которого nglib создала тетраэдрическое разбиение. Вы также можете использовать библиотеку tetlib (tetgen) если установите её в качестве плагина.
Загрузка входного файла:
File Open -> pump_carter_sup.stp
Разбиение займет одну две минуты. Вы должны получить вашу сетку и проверить Model summary . С помощью netgen с настройками по умолчанию генерируется 8371 узла и 36820 тетраэдрических элементов. Визуальный осмотр показал что сетка не совсем удовлетворяет геометрической точности. Мы решили изменить сетку, изменив настройки следующим образом.
View -> Cad model...
Model -> Preferences...
Restrict mesh size on surfaces by STL density = on
Apply
Mesh -> Remesh
Разбиение заняло одну две минуты. Измененная сетка включает 16159 узлов и 65689 тетраэдрических элементов и более не режет глаз. Чтобы влиять на плотность сетки изучайте опции командной строки в руководстве к netgen. Здесь мы продолжим с заданной сеткой.

Figure 3: Рис 2:Расчетная сетка с тремя объеденными границами
Нам необходимо задать температуру на внутренней поверхности отверстий и объединить три границы (смотри рисунок 2 ). Для этой цели мы можем выбрать шесть частей, из которых состоят границы, как показано на картинке, зажав клавишу Ctrl(выбор два клика левой клавишей).
Mesh Unify Surface
После этого у нас есть сетка, мы переходим в меню Model и начинаем идти по пунктам сверху вниз. В Setup мы выбираем вещи связанные с моделированием такие как: имена файлов, временные интервалы(шаги), константы и.т.д. Моделирование осуществляется в трехмерных декартовых координатах и стационарных условиях. Так что необходима только одна стационарная итерация(шаг) , в нашем случае линейная.
Model
Setup
Simulation Type = Steady state
Steady state max. iter = 1
Выберете Apply для того чтобы закрыть окно.
В разделе equation мы выбираем соответствующие уравнения и параметры связанные с решением. В данном случае у нас будет только один набору уравнений – the heat equation.
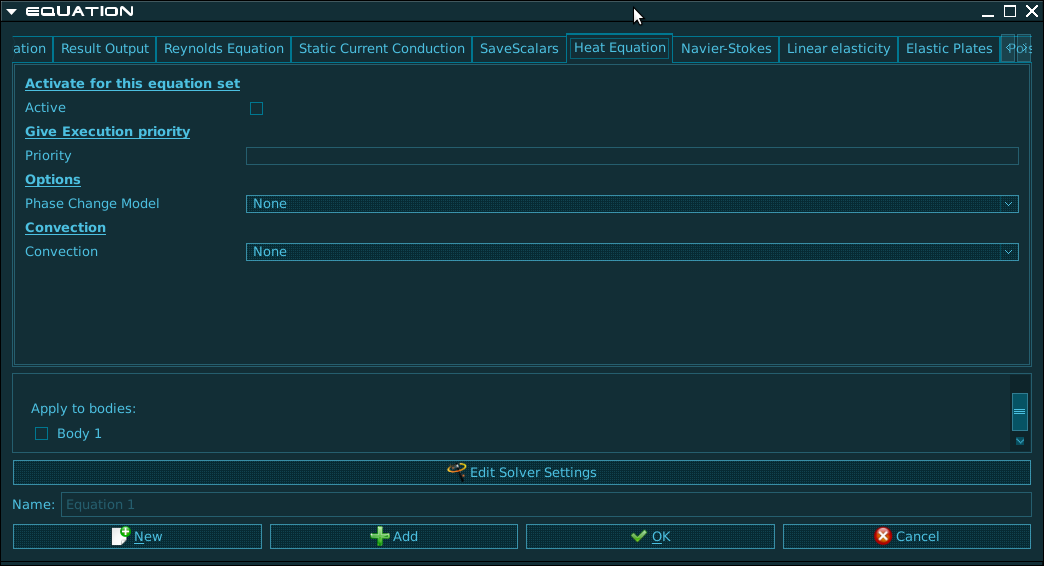
При задании Equations(Уравнений) и Materials можно немедленно назначить тела, или используя мышь выбрать их чуть позже. В нашем случае у нас только одно тело и задать его проще напрямую назначить в Equation and Material , в то время как активную границу мы выбрана графически.
Для решения системы линейных уравнений, мы рады использовать значения по умолчанию. Можно тем не менее, попробовать различные предобуславливатели, например (ILU1, …)
Model
Equation
Add
Name = Heat Equation
Apply to bodies = Body 1
Heat Equation
Active = on
Add
OK
Раздел Material включает в себя все параметры материала. Они делятся на общие параметры, которые является прямыми свойствами материала без каких либо предположений о его физической модели, такой как масса. Остальные свойства зависят от физических законов, таких как теплопроводность. Мы выбрали Алюминий Aluminium из библиотеки материалов Material library которая автоматически установила все необходимы свойства материала.
Model
Material
Add
Material library
Aluminium
Apply to bodies = Body 1
Add
OK
Пункт Body Force представляет из себя правую часть уравнений, которая в нашем случае представляет источник тепла.
Model
Body Force
Add
Name = Heating
Heat Source = 0.01
Apply to bodies = Body 1
Add
OK
Начальные условия не нужны в стационарном случае.
В этом случае мы имеем только одну границу и установим её до комнатной температуры. Сначала зададим граничные условия
Model
BoundaryCondition
Add
Heat Equation
Temperature = 293.0
Name = RoomTemp
Add
OK
Затем зададим граничные свойства
Model Set boundary properties
Выберете определенную группу из трех границ(отверстия) с помощью мыши и примените условия для данных границ.
Boundary condition RoomTemp
Для того чтобы запустить ElmerSolver необходима файл с сеткой и командный файл. Мы знаем что в основном вся информация из ElmerGUI записывается в командный файл. После того как он записан, вы также можете посмотреть файл команд.
Sif Generate Edit -> look how your command file came out
Перед тем как запускать решатель мы должны сохранить файлы в каталоге. В сохраненном проекте будут все необходимые файлы будут сохранены в указанном каталоге.
File Save Project
После того как мы успешно сохранили файлы мы можем запустить решатель
Run Start solver
Автоматически всплывает окно «сходимости» показывающее относительные изменения на каждом шаге. В случае линейного схождения, только одна итерация(шаг) была необходима для получения решения и ещё одна нужна для того чтобы проверить сходимость. Нормальное решение должно быть около 432.4 K (с tetgen, не настроенной, сеткой по умолчанию 389.8 K, соответственно).
Примечание: Если вы столкнетесь с проблемами на каком-то этапе решение и вам надо отредактировать настройки, всегда помните восстанавливайте sif файл и сохраняйте проект перед выполнением.
Постобработка
Чтобы посмотреть результаты вы можете запустить постабработчик ElmerPost или запустить внешний VTK виджет , как это сделано здесь,
Run Postprocessor (VTK)
В конфигурации по умолчанию показывается только объект. Для окрашивания поверхности в соответствии с изменением температуры необходимо выбрать
Surfaces Surface: Temperature Apply
Максимальная температура должна быть около 586.5 K. Вы можете включить opasity для того чтобы видеть сквозь объект, 10-20% это хороший показатель. Таким образом вы будете в состоянии видеть некоторые изоповерхности(равного потенциала/температуры) которые вы можете определить. Некоторые примеры визуализации можно увидеть на рисунке 3
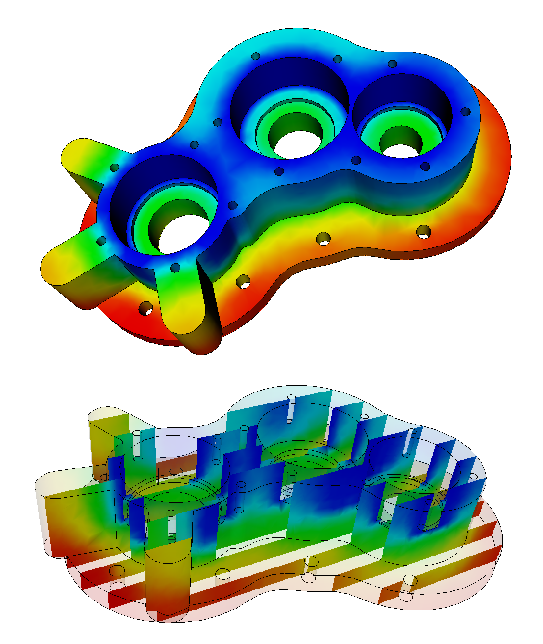
Figure 5: Рис. 3: The temperature distribution of the solid object domain as visualized using the VTK-based postprocessor
Выводы и отсебятина
Задача была в том что есть некоторое тепло генерируемое телом и заданное параметром h, но это интегральный параметр, и чтобы найти распределение температуры по всему телу необходимо использовать уравнение теплопроводности и граничные условия заданные тем что у нас температура на гранях отверстий была комнатной.
Мы увидели три этапа работы с CAE программой, а именно этап разбиения исходного тела на сетку, наиболее приближенную к телу, но при этом не излишнюю в точности. Затем выбор уравнений и задание начальных условий, последний этап это постобработка. Elmer хорош тем что все эти блоки в нем более взаимосвязаны и свои, в отличие от openFOAM о котором мы поговорим позже.
Для создания тел моделей вы можете использовать все то множество свободного софта которое может сохранять модели в STEP например BRL-CAD, Blender ,FreeCAD
Ждем ваших замечаний и предложений!